Latent Variables and Model Mis-specification

Machine learning is very good at optimizing predictions to match an observed signal — for instance, given a dataset of input images and labels of the images (e.g. dog, cat, etc.), machine learning is very good at correctly predicting the label of a new image. However, performance can quickly break down as soon as we care about criteria other than predicting observables. There are several cases where we might care about such criteria:

• In scientific investigations, we often care less about predicting a specific observable phenomenon, and more about what that phenomenon implies about an underlying scientific theory.
• In economic analysis, we are most interested in what policies will lead to desirable outcomes. This requires predicting what would counterfactually happen if we were to enact the policy, which we (usually) don’t have any data about.
• In machine learning, we may be interested in learning value functions which match human preferences (this is especially important in complex settings where it is hard to specify a satisfactory value function by hand). However, we are unlikely to observe information about the value function directly, and instead must infer it implicitly. For instance, one might infer a value function for autonomous driving by observing the actions of an expert driver.

In all of the above scenarios, the primary object of interest — the scientific theory, the effects of a policy, and the value function, respectively — is not part of the observed data. Instead, we can think of it as an unobserved (or “latent”) variable in the model we are using to make predictions. While we might hope that a model that makes good predictions will also place correct values on unobserved variables as well, this need not be the case in general, especially if the model is mis-specified.

I am interested in latent variable inference because I think it is a potentially important sub-problem for building AI systems that behave safely and are aligned with human values. The connection is most direct for value learning, where the value function is the latent variable of interest and the fidelity with which it is learned directly impacts the well-behavedness of the system. However, one can imagine other uses as well, such as making sure that the concepts that an AI learns sufficiently match the concepts that the human designer had in mind. It will also turn out that latent variable inference is related to counterfactual reasoning, which has a large number of tie-ins with building safe AI systems that I will elaborate on in forthcoming posts.

The goal of this post is to explain why problems show up if one cares about predicting latent variables rather than observed variables, and to point to a research direction (counterfactual reasoning) that I find promising for addressing these issues. More specifically, in the remainder of this post, I will: (1) give some formal settings where we want to infer unobserved variables and explain why we can run into problems; (2) propose a possible approach to resolving these problems, based on counterfactual reasoning.

1 Identifying Parameters in Regression Problems

Suppose that we have a regression model , which outputs a probability distribution over given a value for . Also suppose we are explicitly interested in identifying the “true” value of rather than simply making good predictions about given . For instance, we might be interested in whether smoking causes cancer, and so we care not just about predicting whether a given person will get cancer () given information about that person (), but specifically whether the coefficients in that correspond to a history of smoking are large and positive.

In a typical setting, we are given data points on which to fit a model. Most methods of training machine learning systems optimize predictive performance, i.e. they will output a parameter that (approximately) maximizes . For instance, for a linear regression problem we have . Various more sophisticated methods might employ some form of regularization to reduce overfitting, but they are still fundamentally trying to maximize some measure of predictive accuracy, at least in the limit of infinite data.

Call a model well-specified if there is some parameter for which matches the true distribution over , and call a model mis-specified if no such exists. One can show that for well-specified models, maximizing predictive accuracy works well (modulo a number of technical conditions). In particular, maximizing will (asymptotically, as ) lead to recovering the parameter .

However, if a model is mis-specified, then it is not even clear what it means to correctly infer . We could declare the maximizing predictive accuracy to be the “correct” value of , but this has issues:

1. While might do a good job of predicting in the settings we’ve seen, it may not predict well in very different settings.
2. If we care about determining for some scientific purpose, then good predictive accuracy may be an unsuitable metric. For instance, even though margarine consumption might correlate well with (and hence be a good predictor of) divorce rate, that doesn’t mean that there is a causal relationship between the two.

The two problems above also suggest a solution: we will say that we have done a good job of inferring a value for if can be used to make good predictions in a wide variety of situations, and not just the situation we happened to train the model on. (For the latter case of predicting causal relationships, the “wide variety of situations” should include the situation in which the relevant causal intervention is applied.)

Note that both of the problems above are different from the typical statistical problem of overfitting. Clasically, overfitting occurs when a model is too complex relative to the amount of data at hand, but even if we have a large amount of data the problems above could occur. This is illustrated in the following graph:

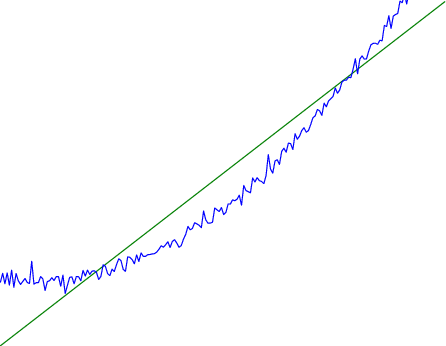
Here the blue line is the data we have (), and the green line is the model we fit (with slope and intercept parametrized by ). We have more than enough data to fit a line to it. However, because the true relationship is quadratic, the best linear fit depends heavily on the distribution of the training data. If we had fit to a different part of the quadratic, we would have gotten a potentially very different result. Indeed, in this situation, there is no linear relationship that can do a good job of extrapolating to new situations, unless the domain of those new situations is restricted to the part of the quadratic that we’ve already seen.

I will refer to the type of error in the diagram above as mis-specification error. Again, mis-specification error is different from error due to overfitting. Overfitting occurs when there is too little data and noise is driving the estimate of the model; in contrast, mis-specification error can occur even if there is plenty of data, and instead occurs because the best-performing model is different in different scenarios.

2 Structural Equation Models

We will next consider a slightly subtler setting, which in economics is referred to as a structural equation model. In this setting we again have an output whose distribution depends on an input , but now this relationship is mediated by an unobserved variable . A common example is a discrete choice model, where consumers make a choice among multiple goods () based on a consumer-specific utility function () that is influenced by demographic and other information about the consumer (). Natural language processing provides another source of examples: in semantic parsing, we have an input utterance () and output denotation (), mediated by a latent logical form ; in machine translation, we have input and output sentences ( and ) mediated by a latent alignment ().

Symbolically, we represent a structural equation model as a parametrized probability distribution , where we are trying to fit the parameters . Of course, we can always turn a structural equation model into a regression model by using the identity , which allows us to ignore altogether. In economics this is called a reduced form model. We use structural equation models if we are specifically interested in the unobserved variable (for instance, in the examples above we are interested in the value function for each individual, or in the logical form representing the sentence’s meaning).

In the regression setting where we cared about identifying , it was obvious that there was no meaningful “true” value of when the model was mis-specified. In this structural equation setting, we now care about the latent variable , which can take on a meaningful true value (e.g. the actual utility function of a given individual) even if the overall model is mis-specified. It is therefore tempting to think that if we fit parameters and use them to impute , we will have meaningful information about the actual utility functions of individual consumers. However, this is a notational sleight of hand — just because we call “the utility function” does not make it so. The variable need not correspond to the actual utility function of the consumer, nor does the consumer’s preferences even need to be representable by a utility function.

We can understand what goes wrong by consider the following procedure, which formalizes the proposal above:

1. Find to maximize the predictive accuracy on the observed data, , where . Call the result .
2. Using this value , treat as being distributed according to . On a new value for which is not observed, treat as being distributed according to .

As before, if the model is well-specified, one can show that such a procedure asymptotically outputs the correct probability distribution over . However, if the model is mis-specified, things can quickly go wrong. For example, suppose that represents what choice of drink a consumer buys, and represents consumer utility (which might be a function of the price, attributes, and quantity of the drink). Now suppose that individuals have preferences which are influenced by unmodeled covariates: for instance, a preference for cold drinks on warm days, while the input does not have information about the outside temperature when the drink was bought. This could cause any of several effects:

• If there is a covariate that happens to correlate with temperature in the data, then we might conclude that that covariate is predictive of preferring cold drinks.
• We might increase our uncertainty about to capture the unmodeled variation in .
• We might implicitly increase uncertainty by moving utilities closer together (allowing noise or other factors to more easily change the consumer’s decision).

In practice we will likely have some mixture of all of these, and this will lead to systematic biases in our conclusions about the consumers’ utility functions.

The same problems as before arise: while we by design place probability mass on values of that correctly predict the observation , under model mis-specification this could be due to spurious correlations or other perversities of the model. Furthermore, even though predictive performance is high on the observed data (and data similar to the observed data), there is no reason for this to continue to be the case in settings very different from the observed data, which is particularly problematic if one is considering the effects of an intervention. For instance, while inferring preferences between hot and cold drinks might seem like a silly example, the design of timber auctions constitutes a much more important example with a roughly similar flavour, where it is important to correctly understand the utility functions of bidders in order to predict their behaviour under alternative auction designs (the model is also more complex, allowing even more opportunities for mis-specification to cause problems).

3 A Possible Solution: Counterfactual Reasoning

In general, under model mis-specification we have the following problems:

• It is often no longer meaningful to talk about the “true” value of a latent variable (or at the very least, not one within the specified model family).
• Even when there is a latent variable with a well-defined meaning, the imputed distribution over need not match reality.

We can make sense of both of these problems by thinking in terms of counterfactual reasoning. Without defining it too formally, counterfactual reasoning is the problem of making good predictions not just in the actual world, but in a wide variety of counterfactual worlds that “could” exist. (I recommend this paper as a good overview for machine learning researchers.)

While typically machine learning models are optimized to predict well on a specific distribution, systems capable of counterfactual reasoning must make good predictions on many distributions (essentially any distribution that can be captured by a reasonable counterfactual). This stronger guarantee allows us to resolve many of the issues discussed above, while still thinking in terms of predictive performance, which historically seems to have been a successful paradigm for machine learning. In particular:

• While we can no longer talk about the “true” value of , we can say that a value of is a “good” value if it makes good predictions on not just a single test distribution, but many different counterfactual test distributions. This allows us to have more confidence in the generalizability of any inferences we draw based on (for instance, if is the coefficient vector for a regression problem, any variable with positive sign is likely to robustly correlate with the response variable for a wide variety of settings).
• The imputed distribution over a variable must also lead to good predictions for a wide variety of distributions. While this does not force to match reality, it is a much stronger condition and does at least mean that any aspect of that can be measured in some counterfactual world must correspond to reality. (For instance, any aspect of a utility function that could at least counterfactually result in a specific action would need to match reality.)
• We will successfully predict the effects of an intervention, as long as that intervention leads to one of the counterfactual distributions considered.

(Note that it is less clear how to actually train models to optimize counterfactual performance, since we typically won’t observe the counterfactuals! But it does at least define an end goal with good properties.)

Many people have a strong association between the concepts of “counterfactual reasoning” and “causal reasoning”. It is important to note that these are distinct ideas; causal reasoning is a type of counterfactual reasoning (where the counterfactuals are often thought of as centered around interventions), but I think of counterfactual reasoning as any type of reasoning that involves making robustly correct statistical inferences across a wide variety of distributions. On the other hand, some people take robust statistical correlation to be the definition of a causal relationship, and thus do consider causal and counterfactual reasoning to be the same thing.

I think that building machine learning systems that can do a good job of counterfactual reasoning is likely to be an important challenge, especially in cases where reliability and safety are important, and necessitates changes in how we evaluate machine learning models. In my mind, while the Turing test has many flaws, one thing it gets very right is the ability to evaluate the accuracy of counterfactual predictions (since dialogue provides the opportunity to set up counterfactual worlds via shared hypotheticals). In contrast, most existing tasks focus on repeatedly making the same type of prediction with respect to a fixed test distribution. This latter type of benchmarking is of course easier and more clear-cut, but fails to probe important aspects of our models. I think it would be very exciting to design good benchmarks that require systems to do counterfactual reasoning, and I would even be happy to incentivize such work monetarily.

Acknowledgements

Thanks to Michael Webb, Sindy Li, and Holden Karnofsky for providing feedback on drafts of this post. If any readers have additional feedback, please feel free to send it my way.

Maximal Maximum-Entropy Sets

Consider a probability distribution on a space . Suppose we want to construct a set of probability distributions on such that is the maximum-entropy distribution over :

where is the entropy. We call such a set a maximum-entropy set for . Furthermore, we would like to be as large as possible, subject to the constraint that is convex.

Does such a maximal convex maximum-entropy set exist? That is, is there some convex set such that is the maximum-entropy distribution in , and for any satisfying the same property, ? It turns out that the answer is yes, and there is even a simple characterization of :

Proposition 1 For any distribution on , the set

is the maximal convex maximum-entropy set for .

To see why this is, first note that, clearly, , and for any we have

so is indeed the maximum-entropy distribution in . On the other hand, let be any other convex set whose maximum-entropy distribution is . Then in particular, for any , we must have . Let us suppose for the sake of contradiction that , so that . Then we have

Since , for sufficiently small this will exceed , which is a contradiction. Therefore we must have for all , and hence , so that is indeed the maximal convex maximum-entropy set for .

Long-Term and Short-Term Challenges to Ensuring the Safety of AI Systems

Introduction

There has been much recent discussion about AI risk, meaning specifically the potential pitfalls (both short-term and long-term) that AI with improved capabilities could create for society. Discussants include AI researchers such as Stuart Russell and Eric Horvitz and Tom Dietterich, entrepreneurs such as Elon Musk and Bill Gates, and research institutes such as the Machine Intelligence Research Institute (MIRI) and Future of Humanity Institute (FHI); the director of the latter institute, Nick Bostrom, has even written a bestselling book on this topic. Finally, ten million dollars in funding have been earmarked towards research on ensuring that AI will be safe and beneficial. Given this, I think it would be useful for AI researchers to discuss the nature and extent of risks that might be posed by increasingly capable AI systems, both short-term and long-term. As a PhD student in machine learning and artificial intelligence, this essay will describe my own views on AI risk, in the hopes of encouraging other researchers to detail their thoughts, as well.

For the purposes of this essay, I will define “AI” to be technology that can carry out tasks with limited or no human guidance, “advanced AI” to be technology that performs substantially more complex and domain-general tasks than are possible today, and “highly capable AI” to be technology that can outperform humans in all or almost all domains. As the primary target audience of this essay is other researchers, I have used technical terms (e.g. weakly supervised learning, inverse reinforcement learning) whenever they were useful, though I have also tried to make the essay more generally accessible when possible.

Outline

I think it is important to distinguish between two questions. First, does artificial intelligence merit the same degree of engineering safety considerations as other technologies (such as bridges)? Second, does artificial intelligence merit additional precautions, beyond those that would be considered typical? I will argue that the answer is yes to the first, even in the short term, and that current engineering methodologies in the field of machine learning do not provide even a typical level of safety or robustness. Moreover, I will argue that the answer to the second question in the long term is likely also yes — namely, that there are important ways in which highly capable artificial intelligence could pose risks which are not addressed by typical engineering concerns.

The point of this essay is not to be alarmist; indeed, I think that AI is likely to be net-positive for humanity. Rather, the point of this essay is to encourage a discussion about the potential pitfalls posed by artificial intelligence, since I believe that research done now can mitigate many of these pitfalls. Without such a discussion, we are unlikely to understand which pitfalls are most important or likely, and thus unable to design effective research programs to prevent them.

A common objection to discussing risks posed by AI is that it seems somewhat early on to worry about such risks, and the discussion is likely to be more germane if we wait to have it until after the field of AI has advanced further. I think this objection is quite reasonable in the abstract; however, as I will argue below, I think we do have a reasonable understanding of at least some of the risks that AI might pose, that some of these will be realized even in the medium term, and that there are reasonable programs of research that can address these risks, which in many cases would also have the advantage of improving the usability of existing AI systems.

Ordinary Engineering

There are many issues related to AI safety that are just a matter of good engineering methodology. For instance, we would ideally like systems that are transparent, modular, robust, and work under well-understood assumptions. Unfortunately, machine learning as a field has not developed very good methodologies for obtaining any of these things, and so this is an important issue to remedy. In other words, I think we should put at least as much thought into building an AI as we do into building a bridge.

Just to be very clear, I do not think that machine learning researchers are bad engineers; looking at any of the open source tools such as Torch, Caffe, MLlib, and others make it clear that many machine learning researchers are also good software engineers. Rather, I think that as a field our methodologies are not mature enough to address the specific engineering desiderata of statistical models (in contrast to the algorithms that create them). In particular, the statistical models obtained from machine learning algorithms tend to be:

1. Opaque: Many machine learning models consist of hundreds of thousands of parameters, making it difficult to understand how predictions are made. Typically, practitioners resort to error analysis examining the covariates that most strongly influence each incorrect prediction. However, this is not a very sustainable long-term solution, as it requires substantial effort even for relatively narrow-domain systems.
2. Monolithic: In part due to their opacity, models act as a black box, with no modularity or encapsulation of behavior. Though machine learning systems are often split into pipelines of smaller models, the lack of encapsulation can make these pipelines even harder to manage than a single large model; indeed, since machine learning models are by design optimized for a particular input distribution (i.e. whatever distribution they are trained on), we end up in a situation where “Changing Anything Changes Everything” [1].
3. Fragile: As another consequence of being optimized for a particular training distribution, machine learning models can have arbitrarily poor performance when that distribution shifts. For instance, Daumé and Marcu [2] show that a named entity classifier with 92% accuracy on one dataset drops to 58% accuracy on a superficially similar dataset. Though such issues are partially addressed by work on transfer learning and domain adaptation [3], these areas are not very developed compared to supervised learning.
4. Poorly understood: Beyond their fragility, understanding when a machine learning model will work is difficult. We know that a model will work if it is tested on the same distribution it is trained on, and have some extensions beyond this case (e.g. based on robust optimization [4]), but we have very little in the way of practically relevant conditions under which a model trained in one situation will work well in another situation. Although they are related, this issue differs from the opacity issue above in that it relates to making predictions about the system’s future behavior (in particular, generalization to new situations), versus understanding the internal workings of the current system.

That these issues plague machine learning systems is likely uncontroversial among machine learning researchers. However, in comparison to research focused on extending capabilities, very little is being done to address them. Research in this area therefore seems particularly impactful, especially given the desire to deploy machine learning systems in increasingly complex and safety-critical situations.

Extraordinary Engineering

Does AI merit additional safety precautions, beyond those that are considered standard engineering practice in other fields? Here I am focusing only on the long-term impacts of advanced or highly capable AI systems.

My tentative answer is yes; there seem to be a few different ways in which AI could have bad effects, each of which seems individually unlikely but not implausible. Even if each of the risks identified so far are not likely, (i) the total risk might be large, especially if there are additional unidentified risks, and (ii) the existence of multiple “near-misses” motivates closer investigation, as it may suggest some underlying principle that makes AI risk-laden. In the sequel I will focus on so-called “global catastrophic” risks, meaning risks that could affect a large fraction of the earth’s population in a material way. I have chosen to focus on these risks because I think there is an important difference between an AI system messing up in a way that harms a few people (which would be a legal liability but perhaps should not motivate a major effort in terms of precautions) and an AI system that could cause damage on a global scale. The latter would justify substantial precautions, and I want to make it clear that this is the bar I am setting for myself.

With that in place, below are a few ways in which advanced or highly capable AI could have specific global catastrophic risks.

Cyber-attacks. There are two trends which taken together make the prospect of AI-aided cyber-attacks seem worrisome. The first trend is simply the increasing prevalence of cyber-attacks; even this year we have seen Russia attack Ukraine, North Korea attack Sony, and China attack the U.S. Office of Personnel Management. Secondly, the “Internet of Things” means that an increasing number of physical devices will be connected to the internet. Assuming that software exists to autonomously control them, many internet-enabled devices such as cars could be hacked and then weaponized, leading to a decisive military advantage in a short span of time. Such an attack could be enacted by a small group of humans aided by AI technologies, which would make it hard to detect in advance. Unlike other weaponizable technology such as nuclear fission or synthetic biology, it would be very difficult to control the distribution of AI since it does not rely on any specific raw materials. Finally, note that even a team with relatively small computing resources could potentially “bootstrap” to much more computing power by first creating a botnet with which to do computations; to date, the largest botnet has spanned 30 million computers and several other botnets have exceeded 1 million.

Autonomous weapons. Beyond cyber-attacks, improved autonomous robotics technology combined with ubiquitous access to miniature UAVs (“drones”) could allow both terrorists and governments to wage a particularly pernicious form of remote warfare by creating weapons that are both cheap and hard to detect or defend against (due to their small size and high maneuverability). Beyond direct malicious intent, if autonomous weapons systems or other powerful autonomous systems malfunction then they could cause a large amount of damage.

Mis-optimization. A highly capable AI could acquire a large amount of power but pursue an overly narrow goal, and end up harming humans or human value while optimizing for this goal. This may seem implausible at face value, but as I will argue below, it is easier to improve AI capabilities than to improve AI values, making such a mishap possible in theory.

Unemployment. It is already the case that increased automation is decreasing the number of available jobs, to the extent that some economists and policymakers are discussing what to do if the number of jobs is systematically smaller than the number of people seeking work. If AI systems allow a large number of jobs to be automated over a relatively short time period, then we may not have time to plan or implement policy solutions, and there could then be a large unemployment spike. In addition to the direct effects on the people who are unemployed, such a spike could also have indirect consequences by decreasing social stability on a global scale.

Opaque systems. It is also already the case that increasingly many tasks are being delegated to autonomous systems, from trades in financial markets to aggregation of information feeds. The opacity of these systems has led to issues such as the 2010 Flash Crash and will likely lead to larger issues in the future. In the long term, as AI systems become increasingly complex, humans may lose the ability to meaningfully understand or intervene in such systems, which could lead to a loss of sovereignty if autonomous systems are employed in executive-level functions (e.g. government, economy).

Beyond these specific risks, it seems clear that, eventually, AI will be able to outperform humans in essentially every domain. At that point, it seems doubtful that humanity will continue to have direct causal influence over its future unless specific measures are put in place to ensure this. While I do not think this day will come soon, I think it is worth thinking now about how we might meaningfully control highly capable AI systems, and I also think that many of the risks posed above (as well as others that we haven’t thought of yet) will occur on a somewhat shorter time scale.

Let me end with some specific ways in which control of AI may be particularly difficult compared to other human-engineered systems:

1. AI may be “agent-like”, which means that the space of possible behaviors is much larger; our intuitions about how AI will act in pursuit of a given goal may not account for this and so AI behavior could be hard to predict.
2. Since an AI would presumably learn from experience, and will likely run at a much faster serial processing speed than humans, its capabilities may change rapidly, ruling out the usual process of trial-and-error.
3. AI will act in a much more open-ended domain. In contrast, our existing tools for specifying the necessary properties of a system only work well in narrow domains. For instance, for a bridge, safety relates to the ability to successfully accomplish a small number of tasks (e.g. not falling over). For these, it suffices to consider well-characterized engineering properties such as tensile strength. For AI, the number of tasks we would potentially want it to perform is large, and it is unclear how to obtain a small number of well-characterized properties that would ensure safety.
4. Existing machine learning frameworks make it very easy for AI to acquire knowledge, but hard to acquire values. For instance, while an AI’s model of reality is flexibly learned from data, its goal/utility function is hard-coded in almost all situations; an exception is some work on inverse reinforcement learning [5], but this is still a very nascent framework. Importantly, the asymmetry between knowledge (and hence capabilities) and values is fundamental, rather than simply a statement about existing technologies. This is because knowledge is something that is regularly informed by reality, whereas values are only weakly informed by reality: an AI which learns incorrect facts could notice that it makes wrong predictions, but the world might never “tell” an AI that it learned the “wrong values”. At a technical level, while many tasks in machine learning are fully supervised or at least semi-supervised, value acquisition is a weakly supervised task.

In summary: there are several concrete global catastrophic risks posed by highly capable AI, and there are also several reasons to believe that highly capable AI would be difficult to control. Together, these suggest to me that the control of highly capable AI systems is an important problem posing unique research challenges.

Long-term Goals, Near-term Research

Above I presented an argument for why AI, in the long term, may require substantial precautionary efforts. Beyond this, I also believe that there is important research that can be done right now to reduce long-term AI risks. In this section I will elaborate on some specific research projects, though my list is not meant to be exhaustive.

1. Value learning: In general, it seems important in the long term (and also in the short term) to design algorithms for learning values / goal systems / utility functions, rather than requiring them to be hand-coded. One framework for this is inverse reinforcement learning [5], though developing additional frameworks would also be useful.
2. Weakly supervised learning: As argued above, inferring values, in contrast to beliefs, is an at most weakly supervised problem, since humans themselves are often incorrect about what they value and so any attempt to provide fully annotated training data about values would likely contain systematic errors. It may be possible to infer values indirectly through observing human actions; however, since humans often act immorally and human values change over time, current human actions are not consistent with our ideal long-term values, and so learning from actions in a naive way could lead to problems. Therefore, a better fundamental understanding of weakly supervised learning — particularly regarding guaranteed recovery of indirectly observed parameters under well-understood assumptions — seems important.
3. Formal specification / verification: One way to make AI safer would be to formally specify desiderata for its behavior, and then prove that these desiderata are met. A major open challenge is to figure out how to meaningfully specify formal properties for an AI system. For instance, even if a speech transcription system did a near-perfect job of transcribing speech, it is unclear what sort of specification language one might use to state this property formally. Beyond this, though there is much existing work in formal verification, it is still extremely challenging to verify large systems.
4. Transparency: To the extent that the decision-making process of an AI is transparent, it should be relatively easy to ensure that its impact will be positive. To the extent that the decision-making process is opaque, it should be relatively difficult to do so. Unfortunately, transparency seems difficult to obtain, especially for AIs that reach decisions through complex series of serial computations. Therefore, better techniques for rendering AI reasoning transparent seem important.
5. Strategic assessment and planning: Better understanding of the likely impacts of AI will allow a better response. To this end, it seems valuable to map out and study specific concrete risks; for instance, better understanding ways in which machine learning could be used in cyber-attacks, or forecasting the likely effects of technology-driven unemployment, and determining useful policies around these effects. It would also be clearly useful to identify additional plausible risks beyond those of which we are currently aware. Finally, thought experiments surrounding different possible behaviors of advanced AI would help inform intuitions and point to specific technical problems. Some of these tasks are most effectively carried out by AI researchers, while others should be done in collaboration with economists, policy experts, security experts, etc.

The above constitute at least five concrete directions of research on which I think important progress can be made today, which would meaningfully improve the safety of advanced AI systems and which in many cases would likely have ancillary benefits in the short term, as well.

Related Work

At a high level, while I have implicitly provided a program of research above, there are other proposed research programs as well. Perhaps the earliest proposed program is from MIRI [6], which has focused on AI alignment problems that arise even in simplified settings (e.g. with unlimited computing power or easy-to-specify goals) in hopes of later generalizing to more complex settings. The Future of Life Institute (FLI) has also published a research priorities document [7, 8] with a broader focus, including non-technical topics such as regulation of autonomous weapons and economic shifts induced by AI-based technologies. I do not necessarily endorse either document, but think that both represent a big step in the right direction. Ideally, MIRI, FLI, and others will all justify why they think their problems are worth working on and we can let the best arguments and counterarguments rise to the top. This is already happening to some extent [9, 10, 11] but I would like to see more of it, especially from academics with expertise in machine learning and AI [12, 13].

In addition, several specific arguments I have advanced are similar to those already advanced by others. The issue of AI-driven unemployment has been studied by Brynjolfsson and McAfee [14], and is also discussed in the FLI research document. The problem of AI pursuing narrow goals has been elaborated through Bostrom’s “paperclipping argument” [15] as well as the orthogonality thesis [16], which states that beliefs and values are independent of each other. While I disagree with the orthogonality thesis in its strongest form, the arguments presented above for the difficulty of value learning can in many cases reach similar conclusions.

Omohundro [17] has argued that advanced agents would pursue certain instrumentally convergent drives under almost any value system, which is one way in which agent-like systems differ from systems without agency. Good [18] was the first to argue that AI capabilities could improve rapidly. Yudkowsky has argued that it would be easy for an AI to acquire power given few initial resources [19], though his example assumes the creation of advanced biotechnology.

Christiano has argued for the value of transparent AI systems, and proposed the “advisor games” framework as a potential operationalization of transparency [20].

Conclusion

To ensure the safety of AI systems, additional research is needed, both to meet ordinary short-term engineering desiderata as well as to make the additional precautions specific to highly capable AI systems. In both cases, there are clear programs of research that can be undertaken today, which in many cases seem to be under-researched relative to their potential societal value. I therefore think that well-directed research towards improving the safety of AI systems is a worthwhile undertaking, with the additional benefit of motivating interesting new directions of research.

Acknowledgments

Thanks to Paul Christiano, Holden Karnofsky, Percy Liang, Luke Muehlhauser, Nick Beckstead, Nate Soares, and Howie Lempel for providing feedback on a draft of this essay.

References

[1] D. Sculley, et al. Machine Learning: The High-Interest Credit Card of Technical Debt. 2014.
[2] Hal Daumé III and Daniel Marcu. Domain adaptation for statistical classifiers. Journal of Artificial Intelligence Research, pages 101–126, 2006.
[3] Sinno J. Pan and Qiang Yang. A survey on transfer learning. IEEE Transactions on Knowledge and Data Engineering, 22(10):1345–1359, 2010.
[4] Dimitris Bertsimas, David B. Brown, and Constantine Caramanis. Theory and applications of robust optimization. SIAM Review, 53(3):464–501, 2011.
[5] Andrew Ng and Stuart Russell. Algorithms for inverse reinforcement learning. In International Conference in Machine Learning, pages 663–670, 2000.
[6] Nate Soares and Benja Fallenstein. Aligning Superintelligence with Human Interests: A Technical Research Agenda. 2014.
[7] Stuart Russell, Daniel Dewey, and Max Tegmark. Research priorities for robust and beneficial artificial intelligence. 2015.
[8] Daniel Dewey, Stuart Russell, and Max Tegmark. A survey of research questions for robust and beneficial AI. 2015.
[9] Paul Christiano. The Steering Problem. 2015.
[10] Paul Christiano. Stable self-improvement as an AI safety problem. 2015.
[11] Luke Muehlhauser. How to study superintelligence strategy. 2014.
[12] Stuart Russell. Of Myths and Moonshine. 2014.
[13] Tom Dietterich and Eric Horvitz. Benefits and Risks of Artificial Intelligence. 2015.
[14] Erik Brynjolfsson and Andrew McAfee. The second machine age: work, progress, and prosperity in a time of brilliant technologies. WW Norton & Company, 2014.
[15] Nick Bostrom (2003). Ethical Issues in Advanced Artificial Intelligence. Cognitive, Emotive and Ethical Aspects of Decision Making in Humans and in Artificial Intelligence.
[16] Nick Bostrom. “The superintelligent will: Motivation and instrumental rationality in advanced artificial agents.” Minds and Machines 22.2 (2012): 71-85.
[17] Stephen M. Omohundro (2008). The Basic AI Drives. Frontiers in Artificial Intelligence and Applications (IOS Press).
[18] Irving J. Good. “Speculations concerning the first ultraintelligent machine.” Advances in computers 6.99 (1965): 31-83.
[19] Eliezer Yudkowsky. “Artificial intelligence as a positive and negative factor in global risk.” Global catastrophic risks 1 (2008): 303.
[20] Paul Christiano. Advisor Games. 2015.

A Fervent Defense of Frequentist Statistics

[Highlights for the busy: de-bunking standard “Bayes is optimal” arguments; frequentist Solomonoff induction; and a description of the online learning framework.]

Short summary. This essay makes many points, each of which I think is worth reading, but if you are only going to understand one point I think it should be “Myth 5″ below, which describes the online learning framework as a response to the claim that frequentist methods need to make strong modeling assumptions. Among other things, online learning allows me to perform the following remarkable feat: if I’m betting on horses, and I get to place bets after watching other people bet but before seeing which horse wins the race, then I can guarantee that after a relatively small number of races, I will do almost as well overall as the best other person, even if the number of other people is very large (say, 1 billion), and their performance is correlated in complicated ways.

If you’re only going to understand two points, then also read about the frequentist version of Solomonoff induction, which is described in “Myth 6″.

Main article. I’ve already written one essay on Bayesian vs. frequentist statistics. In that essay, I argued for a balanced, pragmatic approach in which we think of the two families of methods as a collection of tools to be used as appropriate. Since I’m currently feeling contrarian, this essay will be far less balanced and will argue explicitly against Bayesian methods and in favor of frequentist methods. I hope this will be forgiven as so much other writing goes in the opposite direction of unabashedly defending Bayes. I should note that this essay is partially inspired by some of Cosma Shalizi’s blog posts, such as this one.

This essay will start by listing a series of myths, then debunk them one-by-one. My main motivation for this is that Bayesian approaches seem to be highly popularized, to the point that one may get the impression that they are the uncontroversially superior method of doing statistics. I actually think the opposite is true: I think most statisticans would for the most part defend frequentist methods, although there are also many departments that are decidedly Bayesian (e.g. many places in England, as well as some U.S. universities like Columbia). I have a lot of respect for many of the people at these universities, such as Andrew Gelman and Philip Dawid, but I worry that many of the other proponents of Bayes (most of them non-statisticians) tend to oversell Bayesian methods or undersell alternative methodologies.

If you are like me from, say, two years ago, you are firmly convinced that Bayesian methods are superior and that you have knockdown arguments in favor of this. If this is the case, then I hope this essay will give you an experience that I myself found life-altering: the experience of having a way of thinking that seemed unquestionably true slowly dissolve into just one of many imperfect models of reality. This experience helped me gain more explicit appreciation for the skill of viewing the world from many different angles, and of distinguishing between a very successful paradigm and reality.

If you are not like me, then you may have had the experience of bringing up one of many reasonable objections to normative Bayesian epistemology, and having it shot down by one of many “standard” arguments that seem wrong but not for easy-to-articulate reasons. I hope to lend some reprieve to those of you in this camp, by providing a collection of “standard” replies to these standard arguments.

I will start with the myths (and responses) that I think will require the least technical background and be most interesting to a general audience. Toward the end, I deal with some attacks on frequentist methods that I believe amount to technical claims that are demonstrably false; doing so involves more math. Also, I should note that for the sake of simplicity I’ve labeled everything that is non-Bayesian as a “frequentist” method, even though I think there’s actually a fair amount of variation among these methods, although also a fair amount of overlap (e.g. I’m throwing in statistical learning theory with minimax estimation, which certainly have a lot of overlap in ideas but were also in some sense developed by different communities).

The Myths:

• Bayesian methods are optimal.
• Bayesian methods are optimal except for computational considerations.
• We can deal with computational constraints simply by making approximations to Bayes.
• The prior isn’t a big deal because Bayesians can always share likelihood ratios.
• Frequentist methods need to assume their model is correct, or that the data are i.i.d.
• Frequentist methods can only deal with simple models, and make arbitrary cutoffs in model complexity (aka: “I’m Bayesian because I want to do Solomonoff induction”).
• Frequentist methods hide their assumptions while Bayesian methods make assumptions explicit.
• Frequentist methods are fragile, Bayesian methods are robust.
• Frequentist methods are responsible for bad science
• Frequentist methods are unprincipled/hacky.
• Frequentist methods have no promising approach to computationally bounded inference.

Myth 1: Bayesian methods are optimal. Presumably when most people say this they are thinking of either Dutch-booking or the complete class theorem. Roughly what these say are the following:

Dutch-book argument: Every coherent set of beliefs can be modeled as a subjective probability distribution. (Roughly, coherent means “unable to be Dutch-booked”.)

Complete class theorem: Every non-Bayesian method is worse than some Bayesian method (in the sense of performing deterministically at least as poorly in every possible world).

Let’s unpack both of these. My high-level argument regarding Dutch books is that I would much rather spend my time trying to correspond with reality than trying to be internally consistent. More concretely, the Dutch-book argument says that if for every bet you force me to take one side or the other, then unless I’m Bayesian there’s a collection of bets that will cause me to lose money for sure. I don’t find this very compelling. This seems analogous to the situation where there’s some quant at Jane Street, and they’re about to run code that will make thousands of dollars trading stocks, and someone comes up to them and says “Wait! You should add checks to your code to make sure that no subset of your trades will lose you money!” This just doesn’t seem worth the quant’s time, it will slow down the code substantially, and instead the quant should be writing the next program to make thousands more dollars. This is basically what dutch-booking arguments seem like to me.

Moving on, the complete class theorem says that for any decision rule, I can do better by replacing it with some Bayesian decision rule. But this injunction is not useful in practice, because it doesn’t say anything about which decision rule I should replace it with. Of course, if you hand me a decision rule and give me infinite computational resources, then I can hand you back a Bayesian method that will perform better. But it still might not perform well. All the complete class theorem says is that every local optimum is Bayesan. To be a useful theory of epistemology, I need a prescription for how, in the first place, I am to arrive at a good decision rule, not just a locally optimal one. And this is something that frequentist methods do provide, to a far greater extent than Bayesian methods (for instance by using minimax decision rules such as the maximum-entropy example given later). Note also that many frequentist methods do correspond to a Bayesian method for some appropriately chosen prior. But the crucial point is that the frequentist told me how to pick a prior I would be happy with (also, many frequentist methods don’t correspond to a Bayesian method for any choice of prior; they nevertheless often perform quite well).

Myth 2: Bayesian methods are optimal except for computational considerations. We already covered this in the previous point under the complete class theorem, but to re-iterate: Bayesian methods are locally optimal, not global optimal. Identifying all the local optima is very different from knowing which of them is the global optimum. I would much rather have someone hand me something that wasn’t a local optimum but was close to the global optimum, than something that was a local optimum but was far from the global optimum.

Myth 3: We can deal with computational constraints simply by making approximations to Bayes. I have rarely seen this born out in practice. Here’s a challenge: suppose I give you data generated in the following way. There are a collection of vectors , , , , each with coordinates. I generate outputs , , , in the following way. First I globally select of the coordinates uniformly at random, then I select a fixed vector such that those coordinates are drawn from i.i.d. Gaussians and the rest of the coordinates are zero. Now I set (i.e. is the dot product of with ). You are given and , and your job is to infer . This is a completely well-specified problem, the only task remaining is computational. I know people who have solved this problem using Bayesan methods with approximate inference. I have respect for these people, because doing so is no easy task. I think very few of them would say that “we can just approximate Bayesian updating and be fine”. (Also, this particular problem can be solved trivially with frequentist methods.)

A particularly egregious example of this is when people talk about “computable approximations to Solomonoff induction” or “computable approximations to AIXI” as if such notions were meaningful.

Myth 4: the prior isn’t a big deal because Bayesians can always share likelihood ratios. Putting aside the practical issue that there would in general be an infinite number of likelihood ratios to share, there is the larger issue that for any hypothesis , there is also the hypothesis that matches exactly up to now, and then predicts the opposite of at all points in the future. You have to constrain model complexity at some point, the question is about how. To put this another way, sharing my likelihood ratios without also constraining model complexity (by focusing on a subset of all logically possible hypotheses) would be equivalent to just sharing all sensory data I’ve ever accrued in my life. To the extent that such a notion is even possible, I certainly don’t need to be a Bayesian to do such a thing.

Myth 5: frequentist methods need to assume their model is correct or that the data are i.i.d. Understanding the content of this section is the most important single insight to gain from this essay. For some reason it’s assumed that frequentist methods need to make strong assumptions (such as Gaussianity), whereas Bayesian methods are somehow immune to this. In reality, the opposite is true. While there are many beautiful and deep frequentist formalisms that answer this, I will choose to focus on one of my favorite, which is online learning.

To explain the online learning framework, let us suppose that our data are . We don’t observe until after making a prediction of what will be, and then we receive a penalty based on how incorrect we were. So we can think of this as receiving prediction problems one-by-one, and in particular we make no assumptions about the relationship between the different problems; they could be i.i.d., they could be positively correlated, they could be anti-correlated, they could even be adversarially chosen.

As a running example, suppose that I’m betting on horses and before each race there are other people who give me advice on which horse to bet on. I know nothing about horses, so based on this advice I’d like to devise a good betting strategy. In this case, would be the bets that each of the other people recommend, would be the horse that I actually bet on, and would be the horse that actually wins the race. Then, supposing that (i.e., the horse I bet on actually wins), is the negative of the payoff from correctly betting on that horse. Otherwise, if the horse I bet on doesn’t win, is the cost I had to pay to place the bet.

If I’m in this setting, what guarantee can I hope for? I might ask for an algorithm that is guaranteed to make good bets — but this seems impossible unless the people advising me actually know something about horses. Or, at the very least, one of the people advising me knows something. Motivated by this, I define my regret to be the difference between my penalty and the penalty of the best of the people (note that I only have access to the latter after all rounds of betting). More formally, given a class of predictors , I define

In this case, would have size and the th predictor would just always follow the advice of person . The regret is then how much worse I do on average than the best expert. A remarkable fact is that, in this case, there is a strategy such that shrinks at a rate of . In other words, I can have an average score within of the best advisor after rounds of betting.

One reason that this is remarkable is that it does not depend at all on how the data are distributed; the data could be i.i.d., positively correlated, negatively correlated, even adversarial, and one can still construct an (adaptive) prediction rule that does almost as well as the best predictor in the family.

To be even more concrete, if we assume that all costs and payoffs are bounded by per round, and that there are people in total, then an explicit upper bound is that after rounds, we will be within dollars on average of the best other person. Under slightly stronger assumptions, we can do even better, for instance if the best person has an average variance of about their mean, then the can be replaced with .

It is important to note that the betting scenario is just a running example, and one can still obtain regret bounds under fairly general scenarios; could be continuous and could have quite general structure; the only technical assumption is that be a convex set and that be a convex function of . These assumptions tend to be easy to satisfy, though I have run into a few situations where they end up being problematic, mainly for computational reasons. For an -dimensional model family, typically decreases at a rate of , although under additional assumptions this can be reduced to , as in the betting example above. I would consider this reduction to be one of the crowning results of modern frequentist statistics.

Yes, these guarantees sound incredibly awesome and perhaps too good to be true. They actually are that awesome, and they are actually true. The work is being done by measuring the error relative to the best model in the model family. We aren’t required to do well in an absolute sense, we just need to not do any worse than the best model. Of as long as at least one of the models in our family makes good predictions, that means we will as well. This is really what statistics is meant to be doing: you come up with everything you imagine could possibly be reasonable, and hand it to me, and then I come up with an algorithm that will figure out which of the things you handed me was most reasonable, and will do almost as well as that. As long as at least one of the things you come up with is good, then my algorithm will do well. Importantly, due to the dependence on the dimension of the model family, you can actually write down extremely broad classes of models and I will still successfully sift through them.

Let me stress again: regret bounds are saying that, no matter how the and are related, no i.i.d. assumptions anywhere in sight, we will do almost as well as any predictor in (in particular, almost as well as the best predictor).

Myth 6: frequentist methods can only deal with simple models and need to make arbitrary cutoffs in model complexity. A naive perusal of the literature might lead one to believe that frequentists only ever consider very simple models, because many discussions center on linear and log-linear models. To dispel this, I will first note that there are just as many discussions that focus on much more general properties such as convexity and smoothness, and that can achieve comparably good bounds in many cases. But more importantly, the reason we focus so much on linear models is because we have already reduced a large family of problems to (log-)linear regression. The key insight, and I think one of the most important insights in all of applied mathematics, is that of featurization: given a non-linear problem, we can often embed it into a higher-dimensional linear problem, via a feature map ( denotes -dimensional space, i.e. vectors of real numbers of length ). For instance, if I think that is a polynomial (say cubic) function of , I can apply the mapping , and now look for a linear relationship between and .

This insight extends far beyond polynomials. In combinatorial domains such as natural language, it is common to use indicator features: features that are if a certain event occurs and otherwise. For instance, I might have an indicator feature for whether two words appear consecutively in a sentence, whether two parts of speech are adjacent in a syntax tree, or for what part of speech a word has. Almost all state of the art systems in natural language processing work by solving a relatively simple regression task (typically either log-linear or max-margin) over a rich feature space (often involving hundreds of thousands or millions of features, i.e. an embedding into or ).

A counter-argument to the previous point could be: “Sure, you could create a high-dimensional family of models, but it’s still a parameterized family. I don’t want to be stuck with a parameterized family, I want my family to include all Turing machines!” Putting aside for a second the question of whether “all Turing machines” is a well-advised model choice, this is something that a frequentist approach can handle just fine, using a tool called regularization, which after featurization is the second most important idea in statistics.

Specifically, given any sufficiently quickly growing function , one can show that, given data points, there is a strategy whose average error is at most worse than any estimator . This can hold even if the model class is infinite dimensional. For instance, if consists of all probability distributions over Turing machines, and we let denote the probability mass placed on the th Turing machine, then a valid regularizer would be

If we consider this, then we see that, for any probability distribution over the first Turing machines (i.e. all Turing machines with description length ), the value of is at most . (Here we use the fact that , since and hence .) This means that, if we receive roughly data, we will achieve error within of the best Turing machine that has description length .

Let me note several things here:

• This strategy makes no assumptions about the data being i.i.d. It doesn’t even assume that the data are computable. It just guarantees that it will perform as well as any Turing machine (or distribution over Turing machines) given the appropriate amount of data.
• This guarantee holds for any given sufficiently smooth measurement of prediction error (the update strategy depends on the particular error measure).
• This guarantee holds deterministically, no randomness required (although predictions may need to consist of probability distributions rather than specific points, but this is also true of Bayesian predictions).

Interestingly, in the case that the prediction error is given by the negative log probability assigned to the truth, then the corresponding strategy that achieves the error bound is just normal Bayesian updating. But for other measurements of error, we get different update strategies. Although I haven’t worked out the math, intuitively this difference could be important if the universe is fundamentally unpredictable but our notion of error is insensitive to the unpredictable aspects.

Myth 7: frequentist methods hide their assumptions while Bayesian methods make assumptions explicit. I’m still not really sure where this came from. As we’ve seen numerous times so far, a very common flavor among frequentist methods is the following: I have a model class , I want to do as well as any model in ; or put another way:

Assumption: At least one model in has error at most .
Guarantee: My method will have error at most .

This seems like a very explicit assumption with a very explicit guarantee. On the other hand, an argument I hear is that Bayesian methods make their assumptions explicit because they have an explicit prior. If I were to write this as an assumption and guarantee, I would write:

Assumption: The data were generated from the prior.
Guarantee: I will perform at least as well as any other method.

While I agree that this is an assumption and guarantee of Bayesian methods, there are two problems that I have with drawing the conclusion that “Bayesian methods make their assumptions explicit”. The first is that it can often be very difficult to understand how a prior behaves; so while we could say “The data were generated from the prior” is an explicit assumption, it may be unclear what exactly that assumption entails. However, a bigger issue is that “The data were generated from the prior” is an assumption that very rarely holds; indeed, in many cases the underlying process is deterministic (if you’re a subjective Bayesian then this isn’t necessarily a problem, but it does certainly mean that the assumption given above doesn’t hold). So given that that assumption doesn’t hold but Bayesian methods still often perform well in practice, I would say that Bayesian methods are making some other sort of “assumption” that is far less explicit (indeed, I would be very interested in understanding what this other, more nebulous assumption might be).

Myth 8: frequentist methods are fragile, Bayesian methods are robust. This is another one that’s straightforwardly false. First, since frequentist methods often rest on weaker assumptions they are more robust if the assumptions don’t quite hold. Secondly, there is an entire area of robust statistics, which focuses on being robust to adversarial errors in the problem data.

Myth 9: frequentist methods are responsible for bad science. I will concede that much bad science is done using frequentist statistics. But this is true only because pretty much all science is done using frequentist statistics. I’ve heard arguments that using Bayesian methods instead of frequentist methods would fix at least some of the problems with science. I don’t think this is particularly likely, as I think many of the problems come from mis-application of statistical tools or from failure to control for multiple hypotheses. If anything, Bayesian methods would exacerbate the former, because they often require more detailed modeling (although in most simple cases the difference doesn’t matter at all). I don’t think being Bayesian guards against multiple hypothesis testing. Yes, in some sense a prior “controls for multiple hypotheses”, but in general the issue is that the “multiple hypotheses” are never written down in the first place, or are written down and then discarded. One could argue that being in the habit of writing down a prior might make practitioners more likely to think about multiple hypotheses, but I’m not sure this is the first-order thing to worry about.

Myth 10: frequentist methods are unprincipled / hacky. One of the most beautiful theoretical paradigms that I can think of is what I could call the “geometric view of statistics”. One place that does a particularly good job of show-casing this is Shai Shalev-Shwartz’s PhD thesis, which was so beautiful that I cried when I read it. I’ll try (probably futilely) to convey a tiny amount of the intuition and beauty of this paradigm in the next few paragraphs, although focusing on minimax estimation, rather than online learning as in Shai’s thesis.

The geometric paradigm tends to emphasize a view of measurements (i.e. empirical expected values over observed data) as “noisy” linear constraints on a model family. We can control the noise by either taking few enough measurements that the total error from the noise is small (classical statistics), or by broadening the linear constraints to convex constraints (robust statistics), or by controlling the Lagrange multipliers on the constraints (regularization). One particularly beautiful result in this vein is the duality between maximum entropy and maximum likelihood. (I can already predict the Jaynesians trying to claim this result for their camp, but (i) Jaynes did not invent maximum entropy; (ii) maximum entropy is not particularly Bayesian (in the sense that frequentists use it as well); and (iii) the view on maximum entropy that I’m about to provide is different from the view given in Jaynes or by physicists in general [edit: EHeller thinks this last claim is questionable, see discussion here].)

To understand the duality mentioned above, suppose that we have a probability distribution and the only information we have about it is the expected value of a certain number of functions, i.e. the information that , where the expectation is taken with respect to . We are interested in constructing a probability distribution such that no matter what particular value takes, will still make good predictions. In other words (taking as our measurement of prediction accuracy) we want to be large for all distributions such that . Using a technique called Lagrangian duality, we can both find the optimal distribution and compute its worse-case accuracy over all with . The characterization is as follows: consider all probability distributions that are proportional to for some vector , i.e. for some . Of all of these, take the q(x) with the largest value of . Then will be the optimal distribution and the accuracy for all distributions will be exactly . Furthermore, if is the empirical expectation given some number of samples, then one can show that is propotional to the log likelihood of , which is why I say that maximum entropy and maximum likelihood are dual to each other.

This is a relatively simple result but it underlies a decent chunk of models used in practice.

Myth 11: frequentist methods have no promising approach to computationally bounded inference. I would personally argue that frequentist methods are more promising than Bayesian methods at handling computational constraints, although computationally bounded inference is a very cutting edge area and I’m sure other experts would disagree. However, one point in favor of the frequentist approach here is that we already have some frameworks, such as the “tightening relaxations” framework discussed here, that provide quite elegant and rigorous ways of handling computationally intractable models.

References

(Myth 3) Sparse recovery: Sparse recovery using sparse matrices
(Myth 5) Online learning: Online learning and online convex optimization
(Myth 8) Robust statistics: see this blog post and the two linked papers
(Myth 10) Maximum entropy duality: Game theory, maximum entropy, minimum discrepancy and robust Bayesian decision theory

Convex Conditions for Strong Convexity

An important concept in online learning and convex optimization is that of strong convexity: a twice-differentiable function is said to be strongly convex with respect to a norm if

for all (for functions that are not twice-differentiable, there is an analogous criterion in terms of the Bregman divergence). To check strong convexity, then, we basically need to check a condition on the Hessian, namely that . So, under what conditions does this hold?

For the norm, the answer is easy: if and only if (i.e., is positive semidefinite). This can be shown in many ways, perhaps the easiest is by noting that .

For the norm, the answer is a bit trickier but still not too complicated. Recall that we want necessary and sufficient conditions under which . Note that this is equivalent to asking that for each coordinate of , which in turn is equivalent to for each coordinate vector (these are the vectors that are 1 in the th coordinate and 0 everywhere else).

More generally, for any norm , there exists a dual norm which satisfies, among other properties, the relationship . So, in general, is equivalent to asking that for all with . But this is in turn equivalent to asking that

for all such that .

In fact, it suffices to pick a subset of the such that the convex hull consists of all with ; this is why we were able to obtain such a clean formulation in the case: the dual norm to is , whose unit ball is the simplex, which is a polytope with only vertices (namely, each of the signed unit vectors ).

We can also derive a simple (but computationally expensive) criterion for strong convexity: here the dual norm is , whose unit ball is the -dimensional hypercube, with vertices given by all vectors of the form . Thus if and only if for all sign vectors .

Finally, we re-examine the case; even though the -ball is not a polytope, we were still able to obtain a very simple expression. This was because the condition manages to capture simultaneously all dual vectors such that . We thus have the general criterion:

Theorem. for if and only if is strongly convex with respect to the norm whose dual unit ball is the convex hull of the transformed unit balls , , where is the unit ball whose dimension matches the number of columns of .

Proof.  if and only if . Now note that . If we define , it is then apparent that the dual norm unit ball is the convex hull of the .

Convexity counterexample

Here’s a fun counterexample: a function that is jointly convex in any of the variables, but not in all variables at once. The function is

To see why this is, note that the Hessian of is equal to

This matrix is equal to , where is the identity matrix and is the all-ones matrix, which is rank 1 and whose single non-zero eigenvalue is . Therefore, this matrix has eigenvalues of , as well as a single eigenvalue of , and hence is not positive definite.

On the other hand, any submatrix of size is of the form , but where now is only . This matrix now has eigenvalues of , together with a single eigenvalue of , and hence is positive definite. Therefore, the Hessian is positive definite when restricted to any variables, and hence is convex in any variables, but not in all variables jointly.

Probabilistic Abstractions I

(This post represents research in progress. I may think about these concepts entirely differently a few months from now, but for my own benefit I’m trying to exposit on them in order to force myself to understand them better.)

For many inference tasks, especially ones with either non-linearities or non-convexities, it is common to use particle-based methods such as beam search, particle filters, sequential Monte Carlo, or Markov Chain Monte Carlo. In these methods, we approximate a distribution by a collection of samples from that distribution, then update the samples as new information is added. For instance, in beam search, if we are trying to build up a tree, we might build up a collection of samples for the left and right subtrees, then look at all ways of combining them into the entire tree, but then downsample again to the trees with the highest scores. This allows us to search through the exponentially large space of all trees efficiently (albeit at the cost of possibly missing high-scoring trees).

One major problem with such particle-based methods is diversity: the particles will tend to cluster around the highest-scoring mode, rather than exploring multiple local optima if they exist. This can be bad because it makes learning algorithms overly myopic. Another problem, especially in combinatorial domains, is difficulty of partial evaluation: if we have some training data that we are trying to fit to, and we have chosen settings of some, but not all, variables in our model, it can be difficult to know if that setting is on the right track (for instance, it can be difficult to know whether a partially-built tree is a promising candidate or not). For time-series modeling, this isn’t nearly as large of a problem, since we can evaluate against a prefix of the time series to get a good idea (this perhaps explains the success of particle filters in these domains).

I’ve been working on a method that tries to deal with both of these problems, which I call probabilistic abstractions. The idea is to improve the diversity of particle-based methods by creating “fat” particles which cover multiple states at once; the reason that such fat particles help is that they allow us to first optimize for coverage (by placing down relatively large particles that cover the entire space), then later worry about more local details (by placing down many particles near promising-looking local optima).

To be more concrete, if we have a probability distribution over a set of random variables , then our particles will be sets obtained by specifying the values of some of the and leaving the rest to vary arbitrarily. So, for instance, if , then might be a possible “fat” particle.

By choosing some number of fat particles and assigning probabilities to them, we are implicitly specifying a polytope of possible probability distributions; for instance, if our particles are , and we assign probability to , then we have the polytope of distributions that satisfy the constraints , etc.

Given such a polytope, is there a way to pick a canonical representative from it? One such representative is the maximum entropy distribution in that polytope. This distribution has the property of minimizing the worst-case relative entropy to any other distribution within the polytope (and that worst-case relative entropy is just the entropy of the distribution).

Suppose that we have a polytope for two independent distributions, and we want to compute the polytope for their product. This is easy — just look at the cartesian products of each particle of the first distribution with each particle of the second distribution. If each individual distribution has particles, then the product distribution has particles — this could be problematic computationally, so we also want a way to narrow down to a subset of the most informative particles. These will be the particles such that the corresponding polytope minimizes the maximum entropy of that polytope. Finding this is NP-hard in general, but I’m currently working on good heuristics for computing it.

Next, suppose that we have a distribution on a space and want to apply a function to it. If is a complicated function, it might be difficult to propagate the fat particles (even though it would have been easy to propagate particles composed of single points). To get around this, we need what is called a valid abstraction of : a function such that for all . In this case, if we map a particle to , our equality constraint on the mass assigned to becomes a lower bound on the mass assigned to — we thus still have a polytope of possible probability distributions. Depending on the exact structure of the particles (i.e. the exact way in which the different sets overlap), it may be necessary to add additional constraints to the polytope to get good performance — I feel like I have some understanding of this, but it’s something I’ll need to investigate empirically as well. It’s also interesting to note that (when combined with conditioning on data, which is discussed below) allows us to assign partial credit to promising particles, which was the other property I discussed at the beginning.

Finally, suppose that I want to condition on data. In this case the polytope approach doesn’t work as well, because conditioning on data can blow up the polytope by an arbitrarily large amount. Instead, we just take the maximum-entropy distribution in our polytope and treat that as our “true” distribution, then condition. I haven’t been able to make any formal statements about this procedure, but it seems to work at least somewhat reasonably. It is worth noting that conditioning may not be straightforward, since the likelihood function may not be constant across a given fat particle. To deal with this, we can replace the likelihood function by its average (which I think can be justified in terms of maximum entropy as well, although the details here are a bit hazier).

So, in summary, we have a notion of fat particles, which provide better coverage than point particles, and can combine them, apply functions to them, subsample them, and condition on data. This is essentially all of the operations we want to be able to apply for particle-based methods, so we in theory should now be able to implement versions of these particle-based methods that get better coverage.

Pairwise Independence vs. Independence

For collections of independent random variables, the Chernoff bound and related bounds give us very sharp concentration inequalities — if are independent, then their sum has a distribution that decays like . For random variables that are only pairwise independent, the strongest bound we have is Chebyshev’s inequality, which says that their sum decays like .

The point of this post is to construct an equality case for Chebyshev: a collection of pairwise independent random variables whose sum does not satisfy the concentration bound of Chernoff, and instead decays like .

The construction is as follows: let be independent binary random variables, and for any , let , where the sum is taken mod 2. Then we can easily check that the are pairwise independent. Now consider  the random variable . If any of the is equal to 1, then we can pair up the by either adding or removing from to get the other element of the pair. If we do this, we see that in this case. On the other hand, if all of the are equal to 0, then as well. Thus, with probability , deviates from its mean by , whereas the variance of is . The bound on this probability form Chebyshev is , which is very close to , so this constitutes something very close to the Chebyshev equality case.

Anyways, I just thought this was a cool example that demonstrates the difference between pairwise and full independence.

Local KL Divergence

The KL divergence is an important tool for studying the distance between two probability distributions. Formally, given two distributions and , the KL divergence is defined as

Note that . Intuitively, a small KL(p || q) means that there are few points that p assigns high probability to but that q does not. We can also think of KL(p || q) as the number of bits of information needed to update from the distribution q to the distribution p.

Suppose that p and q are both mixtures of other distributions: and . Can we bound in terms of the ? In some sense this is asking to upper bound the KL divergence in terms of some more local KL divergence. It turns out this can be done:

Theorem: If and and are all probability distributions, then

.

Proof: If we expand the definition, then we are trying to prove that

We will in fact show that this is true for every value of , so that it is certainly true for the integral. Using , re-write the condition for a given value of as

(Note that the sign of the inequality flipped because we replaced the two expressions with their negatives.) Now, this follows by using Jensen’s inequality on the function:

This proves the inequality and therefore the theorem.

Remark: Intuitively, if we want to describe in terms of , it is enough to first locate the th term in the sum and then to describe in terms of . The theorem is a formalization of this intuition. In the case that , it also says that the KL divergence between two different mixtures of the same set of distributions is at most the KL divergence between the mixture weights.

Exponential Families

In my last post I discussed log-linear models. In this post I’d like to take another perspective on log-linear models, by thinking of them as members of an exponential family. There are many reasons to take this perspective: exponential families give us efficient representations of log-linear models, which is important for continuous domains; they always have conjugate priors, which provide an analytically tractable regularization method; finally, they can be viewed as maximum-entropy models for a given set of sufficient statistics. Don’t worry if these terms are unfamiliar; I will explain all of them by the end of this post. Also note that most of this material is available on the Wikipedia page on exponential families, which I used quite liberally in preparing the below exposition.

1. Exponential Families

An exponential family is a family of probability distributions, parameterized by , of the form

Notice the similarity to the definition of a log-linear model, which is

So, a log-linear model is simply an exponential family model with . Note that we can re-write the right-hand-side of (1) as , so an exponential family is really just a log-linear model with one of the coordinates of constrained to equal . Also note that the normalization constant in (1) is a function of (since fully specifies the distribution over ), so we can express (1) more explicitly as

where

Exponential families are capable of capturing almost all of the common distributions you are familiar with. There is an extensive table on Wikipedia; I’ve also included some of the most common below:

1. Gaussian distributions. Let . Then . If we let , then . We therefore see that Gaussian distributions are an exponential family for .
2. Poisson distributions. Let and . Then . If we let then we get ; we thus see that Poisson distributions are also an exponential family.
3. Multinomial distributions. Suppose that . Let be an -dimensional vector whose th element is and where all other elements are zero. Then . If , then we obtain an arbitrary multinomial distribution. Therefore, multinomial distributions are also an exponential family.

2. Sufficient Statistics

A statistic of a random variable is any deterministic function of that variable. For instance, if is a vector of Gaussian random variables, then the sample mean and sample variance are both statistics.

Let be a family of distributions parameterized by , and let be a random variable with distribution given by some unknown . Then a vector of statistics are called sufficient statistics for if they contain all possible information about , that is, for any function , we have

for some function that has no dependence on .

For instance, let be a vector of independent Gaussian random variables with unknown mean and variance . It turns out that is a sufficient statistic for and . This is not immediately obvious; a very useful tool for determining whether statistics are sufficient is the Fisher-Neyman factorization theorem:

Theorem 1 (Fisher-Neyman) Suppose that has a probability density function . Then the statistics are sufficient for if and only if can be written in the form

In other words, the probability of can be factored into a part that does not depend on , and a part that depends on only via .

What is going on here, intuitively? If depended only on , then would definitely be a sufficient statistic. But that isn’t the only way for to be a sufficient statistic — could also just not depend on at all, in which case would trivially be a sufficient statistic (as would anything else). The Fisher-Neyman theorem essentially says that the only way in which can be a sufficient statistic is if its density is a product of these two cases.

Proof: If (6) holds, then we can check that (5) is satisfied:

where the right-hand-side has no dependence on .

On the other hand, if we compute for an arbitrary density , we get

If the right-hand-side cannot depend on for any choice of , then the term that we multiply by must not depend on ; that is, must be some function that depends only on and and not on . On the other hand, the denominator depends only on and ; call this dependence . Finally, note that is a deterministic function of , so let . We then see that , which is the same form as (6), thus completing the proof of the theorem.

Now, let us apply the Fisher-Neyman theorem to exponential families. By definition, the density for an exponential family factors as

If we let and , then the Fisher-Neyman condition is met; therefore, is a vector of sufficient statistics for the exponential family. In fact, we can go further:

Theorem 2 Let be drawn independently from an exponential family distribution with fixed parameter . Then the empirical expectation is a sufficient statistic for .

Proof: The density for given is

Letting and , we see that the Fisher-Neyman conditions are satisfied, so that is indeed a sufficient statistic.

Finally, we note (without proof) the same relationship as in the log-linear case to the gradient and Hessian of with respect to the model parameters:

Theorem 3 Again let be drawn from an exponential family distribution with parameter . Then the gradient of with respect to is

and the Hessian is

This theorem provides an efficient algorithm for fitting the parameters of an exponential family distribution (for details on the algorithm, see the part near the end of the log-linear models post on parameter estimation).

3. Moments of an Exponential Family

If is a real-valued random variable, then the th moment of is . In general, if is a random variable on , then for every sequence of non-negative integers, there is a corresponding moment .

In exponential families there is a very nice relationship between the normalization constant and the moments of . Before we establish this relationship, let us define the moment generating function of a random variable as .

Lemma 4 The moment generating function for a random variable is equal to

The proof of Lemma 4 is a straightforward application of Taylor’s theorem, together with linearity of expectation (note that in one dimension, the expression in Lemma 4 would just be ).

We now see why is called the moment generating function: it is the exponential generating function for the moments of . The moment generating function for the sufficient statistics of an exponential family is particularly easy to compute:

Lemma 5 If , then .

Proof:

where the last step uses the fact that is a probability density and hence .

Now, by Lemma 4, is just the coefficient in the Taylor series for the moment generating function , and hence we can compute as . Combining this with Lemma 5 gives us a closed-form expression for in terms of the normalization constant :

Lemma 6 The moments of an exponential family can be computed as

For those who prefer cumulants to moments, I will note that there is a version of Lemma 6 for cumulants with an even simpler formula.

Exercise: Use Lemma 6 to compute , where is a Gaussian with mean and variance .

4. Conjugate Priors

Given a family of distributions , a conjugate prior family is a family that has the property that

for some depending on and . In other words, if the prior over lies in the conjugate family, and we observe , then the posterior over also lies in the conjugate family. This is very useful algebraically as it means that we can get our posterior simply by updating the parameters of the prior. The following are examples of conjugate families:

1. (Gaussian-Gaussian) Let , and let . Then, by Bayes’ rule,

Therefore, parameterize a family of priors over that is conjugate to .

• (Beta-Bernoulli) Let , , , and . The distribution over given is then called a Bernoulli distribution, and that of given and is called a beta distribution. Note that can also be written as . From this, we see that the family of beta distributions is a conjugate prior to the family of Bernoulli distributions, since

• (Gamma-Poisson) Let for . Let . As noted before, the distribution for given is called a Poisson distribution; the distribution for given and is called a gamma distribution. We can check that the family of gamma distributions is conjugate to the family of Poisson distributions.Important note: unlike in the last two examples, the normalization constant for the Poisson distribution actually depends on , and so we need to include it in our calculations:

  

  Note that, in general, a family of distributions will always have some conjugate family, as if nothing else the family of all probability distributions over will be a conjugate family. What we really care about is a conjugate family that itself has nice properties, such as tractably computable moments.

  Conjugate priors have a very nice relationship to exponential families, established in the following theorem:

  Theorem 7 Let be an exponential family. Then is a conjugate prior for for any choice of . The update formula is . Furthermore, is itself an exponential family, with sufficient statistics .

  Checking the theorem is a matter of straightforward algebra, so I will leave the proof as an exercise to the reader. Note that, as before, there is no guarantee that will be tractable; however, in many cases the conjugate prior given by Theorem 7 is a well-behaved family. See this Wikipedia page for examples of conjugate priors, many of which correspond to exponential family distributions.

  5. Maximum Entropy and Duality

  The final property of exponential families I would like to establish is a certain duality property. What I mean by this is that exponential families can be thought of as the maximum entropy distributions subject to a constraint on the expected value of their sufficient statistics. For those unfamiliar with the term, the entropy of a distribution over with density is . Intuitively, higher entropy corresponds to higher uncertainty, so a maximum entropy distribution is one specifying as much uncertainty as possible given a certain set of information (such as the values of various moments). This makes them appealing, at least in theory, from a modeling perspective, since they “encode exactly as much information as is given and no more”. (Caveat: this intuition isn’t entirely valid, and in practice maximum-entropy distributions aren’t always necessarily appropriate.)

  In any case, the duality property is captured in the following theorem:

  Theorem 8 The distribution over with maximum entropy such that lies in the exponential family with sufficient statistic and .

  Proving this fully rigorously requires the calculus of variations; I will instead give the “physicist’s proof”. Proof: } Let be the density for . Then we can view as the solution to the constrained maximization problem:

  

  By the method of Lagrange multipliers, there exist and such that

  

  This simplifies to:

  

  which implies

  

  for some and . In particular, if we let and , then we recover the exponential family with , as claimed.

  6. Conclusion

  Hopefully I have by now convinced you that exponential families have many nice properties: they have conjugate priors, simple-to-fit parameters, and easily-computed moments. While exponential families aren’t always appropriate models for a given situation, their tractability makes them the model of choice when no other information is present; and, since they can be obtained as maximum-entropy families, they are actually appropriate models in a wide family of circumstances.